Here are some basic definitions and properties of lines and angles in geometry. These concepts are tested in many competitive entrance exams like GMAT, GRE, CAT.
These essential geometry concepts form the base on which more complex ideas can be built. Don’t worry if you haven’t had any exposure to it earlier.
We’ll start off with the most simple ideas and then build the other related theory over it.
Bookmark this page for easy reference, so you can come back to it anytime you feel you need a refresher course on lines and angles.
Line segment: A line segment has two end points with a definite length.
Ray: A ray has one end point and infinitely extends in one direction.
Straight line: A straight line has neither starting nor end point and is of infinite length.
Acute angle: The angle that is between 0° and 90° is an acute angle, ∠A in the figure below.

Obtuse angle: The angle that is between 90° and 180° is an obtuse angle, ∠B as shown below.

Right angle: The angle that is 90° is a Right angle, ∠C as shown below.

Straight angle: The angle that is 180° is a straight angle, ∠AOB in the figure below.
Supplementary angles:

In the figure above, ∠AOC + ∠COB = ∠AOB = 180°
If the sum of two angles is 180° then the angles are called supplementary angles.
Two right angles always supplement each other.
The pair of adjacent angles whose sum is a straight angle is called a linear pair.
Complementary angles:

∠COA + ∠AOB = 90°
If the sum of two angles is 90° then the two angles are called complementary angles.
Adjacent angles:
The angles that have a common arm and a common vertex are called adjacent angles.
In the figure above, ∠BOA and ∠AOC are adjacent angles. Their common arm is OA and common vertex is ‘O’.
Vertically opposite angles:
When two lines intersect, the angles formed opposite to each other at the point of intersection (vertex) are called vertically opposite angles.

In the figure above,
x and y are two intersecting lines.
∠A and ∠C make one pair of vertically opposite angles and
∠B and ∠D make another pair of vertically opposite angles.
Perpendicular lines: When there is a right angle between two lines, the lines are said to be perpendicular to each other.

Here, the lines OA and OB are said to be perpendicular to each other.
Parallel lines:

Here, A and B are two parallel lines, intersected by a line p.
The line p is called a transversal, that which intersects two or more lines (not necessarily parallel lines) at distinct points.
As seen in the figure above, when a transversal intersects two lines, 8 angles are formed.
Let us consider the details in a tabular form for easy reference.
| Types of Angles | Angles |
| Interior Angles | ∠3, ∠4, ∠5, ∠6 |
| Exterior Angles | ∠1, ∠2, ∠7, ∠8 |
| Vertically opposite Angles | (∠1, ∠3), (∠2, ∠4), (∠5, ∠7), (∠6, ∠8) |
| Corresponding Angles | (∠1, ∠5), (∠2, ∠6), (∠3, ∠7), (∠4, ∠8) |
| Interior Alternate Angles | (∠3, ∠5), (∠4, ∠6) |
| Exterior Alternate Angles | (∠1, ∠7), (∠2, ∠8) |
| Interior Angles on the same side of transversal | (∠3, ∠6), (∠4, ∠5) |
When a transversal intersects two parallel lines,
- The corresponding angles are equal.
- The vertically opposite angles are equal.
- The alternate interior angles are equal.
- The alternate exterior angles are equal.
- The pair of interior angles on the same side of the transversal is supplementary.
We can say that the lines are parallel if we can verify at least one of the aforementioned conditions.
Let us take a look at some examples.
Solved examples
Example 1. If the lines m and n are parallel to each other, then determine the angles ∠5 and ∠7.
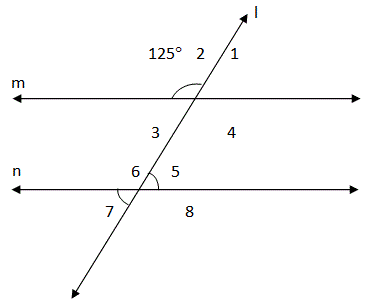
Solution:
Determining one pair can make it possible to find all the other angles. The following is one of the many ways to solve this question.
∠2 = 125°
∠2 = ∠4 since they are vertically opposite angles.
Therefore, ∠4 = 125°
∠4 is one of the interior angles on the same side of the transversal.
Therefore, ∠4 + ∠5 = 180°
125 + ∠5 = 180 → ∠5 = 180 – 125 = 55°
∠5 = ∠7 since vertically opposite angles.
Therefore, ∠5 = ∠7 = 55°
Note: Sometimes, the parallel property of the lines may not be mentioned in the problem statement and the lines may seem to be parallel to each other; but they may be not. It is important to determine whether two lines are parallel by verifying the angles and not by looks.
Example 2. If ∠A = 120° and ∠H = 60°. Determine if the lines are parallel.

Solution:
Given ∠A = 120° and ∠H = 60°.
Since adjacent angles are supplementary, ∠A + ∠B = 180°
120 + ∠B = 180 → ∠B = 60°.
It is given that ∠H = 60°. We can see that ∠B and ∠H are exterior alternate angles.
When exterior alternate angles are equal, the lines are parallel.
Hence the lines p and q are parallel.
We can verify this using other angles.
If ∠H = 60°, ∠E = 120° since those two are on a straight line, they are supplementary.
Now, ∠A = ∠E = 120°. ∠A and ∠E are corresponding angles.
When corresponding angles are equal, the lines are parallel.
Likewise, we can prove using other angles too.
Example 3. If p and q are two lines parallel to each other and ∠E = 50°, find all the angles in the figure below.

Solution:
It is given ∠E = 50°.
The two lines are parallel
→ The corresponding angles are equal.
Since ∠E and ∠A are corresponding angles, ∠A = 50° .
→ The vertically opposite angles are equal.
Since ∠A and ∠C are vertically opposite to each other, ∠C = 50°.
Since ∠E and ∠G are vertically opposite to each other, ∠G = 50°.
→ The interior angles on the same side of the transversal are supplementary.
∠E + ∠D = 180° → 50 + ∠D = 180° → ∠D = 130°
→ ∠D and ∠B are vertically opposite angles. So ∠B = 130°.
→ ∠B and ∠F are corresponding angles. So ∠F = 130°.
→ ∠F and ∠H are vertically opposite angles. So ∠H = 130°.
∠D = ∠O + 90° → 130 = ∠O + 90 → ∠O = 40°
Continue learning:
– Properties and formulas of Circles
– Types of Triangles and Properties
– Properties of Quadrilaterals (parallelograms, trapezium, rhombus)

your website help us to understand the concept better than our tution teachers
thanking you heartly